Nas postagens anteriores já falamos de soma, subtração e multiplicação de polinômios e, agora, chegou a vez de falarmos da divisão de polinômios. A divisão de polinômios ficou para depois pois precisamos da definição de grau para para explorarmos bem as características da divisão de polinômios. A divisão de polinômios costuma a assustar um pouco as pessoas pois parece uma coisa complicada, mas na verdade não é. Nessa postagem vamos falar do Algoritmo da Divisão para polinômios que é o teorema que garante a possibilidade de se fazer a divisão e, depois disso, vamos ver exemplos de como se fazer a divisão de polinômios. Vamos lá!
Algoritmo da divisão para polinômios
Antes de fazermos os exemplos de divisão de polinômios, vamos abordar a teoria por trás dessa operação. Vamos ver agora o teorema chamado Algoritmo da Divisão para polinômios, que também é conhecido como Algoritmo de Euclides para polinômios. Esse teorema nos garante que sempre é possível dividir um polinômios por outro, que não seja nulo.
Teorema: (Algoritmo da Divisão para polinômios) Dados os polinômios $f(x)$ e $g(x)$ (sobre $\mathbb{R}$ ou sobre $\mathbb{C}$) com $g(x) \neq 0$, então existem polinômios $q(x)$ e $r(x)$ (sobre o mesmo conjunto nos quais $f(x)$ e $g(x)$ estão) tais que $f(x) = g(x) \cdot q(x) + r(x)$ onde $r(x) = 0$ ou $gr(r(x)) < gr(g(x))$. Além disso, os polinômios $q(x)$ e $r(x)$ são únicos.
Observação: Os polinômios $q(x)$ e $r(x)$ do teorema anterior são chamado de quociente e resto, respectivamente, da divisão de $f(x)$ por $g(x)$. Também chamamos o polinômio $f(x)$ de dividendo e o polinômio $g(x)$ de divisor.
Em outras palavras, o que o Algoritmo da Divisão para polinômios está nos dizendo é o seguinte, se você tem dois polinômios $f(x)$ e $g(x)$, com $g(x) \neq 0$, e precisa dividir $f(x)$ por $g(x)$, então você conseguirá encontrar um quociente $q(x)$ e um resto $r(x)$, únicos, tais que $f(x) = g(x) \cdot q(x) + r(x)$ onde $r(x) = 0$ ou $gr(r(x)) < gr(g(x))$.
No caso em que, na divisão de $f(x)$ por $g(x)$ obtivermos $r(x) = 0$, ou seja, o resto da divisão é o polinômio nulo, dizemos que $g(x)$ divide $f(x)$.
O Algoritmo da Divisão para polinômios nos garante que sempre é possível fazer a divisão de um polinômio por outro não nulo, porém ele não nos apresenta nenhuma forma de encontrarmos o quociente $q(x)$ e o resto $r(x)$. A seguir veremos exemplos de como dividir dois polinômios e obtermos o quociente e o resto dessa divisão.
Exemplos:
1. Calcule o quociente e o resto na divisão de $f(x) = x^3-2x^2+x + 4$ por $g(x) = x+2$.
Solução: Começaremos a fazer esta divisão montando a chave com os polinômios, da seguinte forma:
Depois de montarmos a chave, vamos começar a determinar o quociente $q(x)$ que vai estar na seguinte posição na chave:
Para começarmos a calcular o quociente, precisamos olhar o primeiro termo de $f(x)$ e o primeiro termo de $g(x)$, que são, respectivamente, $x^3$ e $x$. Tendo identificados esses temos, temos que encontrar um termo de $q(x)$ tal que, este termo multiplicado por $x$, seja igual a $x^3$ (isto é, o primeiro termo de $q(x)$ deve ser o termo que multiplicado pelo primeiro termo de $g(x)$ seja igual ao primeiro termo de $f(x)$). Podemos perceber que o primeiro termo de $q(x)$ será então $x^2$, pois, $x^3 = x^2 \cdot x$. Agora que determinamos o primeiro termo de $q(x)$, vamos começar a escrever o $q(x)$.
Agora vamos multiplicar $x^2$ por $g(x) = x+2$ e vamos colocar o resultado em baixo de $f(x)$, da direita para a esquerda, de modo que as mesmas potências de $x$ fiquem uma em baixo da outra. Veja que $x^2(x+2) = x^3 + 2x^2$.
Agora vamos fazer $f(x) - (x^3 + 2x^2)$.
Depois de efetuarmos a subtração, encontramos o polinômio $-4x^2+x+4$. Vamos continuar obtendo o quociente $q(x)$ da seguinte forma, vamos determinar o próximo termo de $q(x)$ tal que, multiplicado pelo primeiro termo de $g(x) = x+2$, se obtenha o primeiro termo de $-4x^2+x+4$. Isto é, queremos encontrar um outro termo de $q(x)$ tal que, ele vezes $x$ seja igual a $-4x^2$. Logo, este termo que estamos procurando é igual a $-4x$. Vamos colocar esse termo logo após $x^2$ do quociente.
Agora, vamos multiplicar $-4x$ por $x+2$, que é igual a $-4x^2-8x$, e colocar em baixo de $-4x^2+x+4$, da direita para a esquerda, de modo que as mesmas potências de $x$ fiquem uma em baixo da outra.
Vamos fazer a subtração $-4x^2 + x + 4 - (-4x^2-8x)$.
Agora nós temos o polinômio $9x+4$. Para prosseguir determinando $q(x)$, devemos encontrar outro termo do polinômio $q(x)$ tal que, este termo multiplicado pelo primeiro termo de $x+2$ seja igual ao primeiro termo de $9x+4$, isto é, o próximo termo de $q(x)$ é tal que ele vezes $x$ é igual a $9x$. Claramente, ele é igual a $9$. Vamos colocá-lo em sequência em $q(x)$.
O próximo passo agora é multiplicar $9$ por $x+2$ e colocar em baixo de $9x+4$ e subtrair um do outro. Note que $9(x+2) = 9x+18$.
Assim, chegamos ao $-14$ e paramos o processo de divisão. Temos que parar por aqui por que chagamos a um resultado das subtrações que possui grau menor que o dividendo, o polinômio $g(x)$. Observe que $gr(-14) = 0$ e $gr(x+2) =1$. Logo, $r(x) = -14$ é o resto da divisão de $f(x)$ por $g(x)$ e $q(x) = x^2-4x+9$ é o quociente, pelo Algoritmo da Divisão para polinômios podemos escrever
$$x^3-2x^2+x+4 = (x+2) \cdot (x^2-4x+9) + (-14).$$
O exemplo anterior foi feito de forma bem detalhada. Vamos fazer o próximo exemplo com menos detalhes pois, como é a mesma operação de divisão de polinômios, será feita de modo análogo ao primeiro exemplo.
2. Calcule o quociente e o resto na divisão de $f(x) = 2x^5 + x^4 + x^3-2x^2+x-4$ por $g(x) = x^2-2x-3$.
Solução: Assim como no início do exemplo anterior, vamos montar a chave com os polinômios do enunciado onde $f(x) = 2x^5 + x^4 + x^3-2x^2+x-4$ é o dividendo e $g(x) = x^2-2x-3$ é o divisor.
O primeiro termo do quociente $q(x)$ é o termo que, multiplicado pelo primeiro termo de $g(x) = x^2-2x-3$ é igual ao primeiro termo de $f(x) = 2x^5 + x^4 + x^3-2x^2+x-4$. Desse modo, temos que o primeiro termo de $q(x)$ é $2x^3$, visto que $2x^3 \cdot x^2 = 2x^5$. Tendo determinado o primeiro termo de $q(x)$, vamos multiplicar esse termo por $g(x) = x^2-2x-3$ e vamos subtrair o resultado de $f(x) = 2x^5 + x^4 + x^3-2x^2+x-4$. Assim vamos obter,
Como resultado da subtração feita anteriormente obtivemos o polinômio $5x^4+7x^3-2x^2$. Assim, o próximo termo de $q(x)$ é tal que, multiplicado pelo primeiro termo de $g(x) = x^2-2x-3$ obtém-se o primeiro termo de $5x^4+7x^3-2x^2$ . Assim, esse próximo termo é igual a $5x^2$ pois $5x^4 = 5x^2 \cdot x^2$. Vamos colocar este termo em sequência no quociente, multiplicar $g(x) = x^2-2x-3$ e subtrair de $5x^4+7x^3-2x^2$. Desse modo, vamos ter,
Essa última subtração ainda não tem resultado com grau menor que o grau do divisor, então vamos continuar a divisão. O próximo termo de $q(x)$, quando multiplicado por $x^2$, deve ser igual a $47x^2$. Sendo assim, esse termo é igual a $47$. Assim, a continuação da divisão fica com a forma
Agora sim acabou a divisão. Observe que o resultado da última subtração é $146x-137$ que possui grau$1$ e, por sua vez, é menor que $2$ que o grau de $g(x) = x^2-2x-3$. Portanto o quociente da divisão é $q(x) = 2x^3 + 5x^2 + 17x+47$ e o resto é $r(x) = 146x + 137$. Pelo Algoritmo da Divisão para polinômios também podemos escrever
$$2x^5 + x^4 + x^3-2x^2+x-4 = (x^2-2x-3) \cdot (2x^3 + 5x^2 + 17x+47) + 146x + 137.$$
Vamos para mais um exemplo.
3. Verifique se o polinômio $x-1$ divide o polinômio $x^3-1$.
Solução: Acima no texto está a definição de quando um polinômio divide outro, que nos diz que isso ocorre se o resto da divisão for igual a zero. Assim, o exercício acima pode ser reescrito acima como: Verifique se o resto da divisão de $x^3-1$ por $x-1$ é igual a $0$. Para verificar isso, vamos efetuar a divisão de $x^3-1$ por $x-1$. Antes disso, observe que $x^3-1$ não está na forma "completa" como os polinômios dos exemplos anteriores, ou seja, ele não possui os termos onde $x$ possui potências $2$ e $1$. Para evitar erros na divisão de um polinômio assim, complete-o com zeros, isto é, o escreva na forma $x^3 + 0x^2 + 0x -1$. Tendo observado isso, vamos fazer a divisão.
A partir de agora, vamos seguir de forma análoga aos exemplos anteriores. Observe que $x^2 \cdot x = x^3$, assim, o primeiro termo do quociente é igual a $x^2$. Multiplicando $x^2$ por $x-1$ vamos ter
A última subtração teve como resulta o $0$, assim a divisão acabou com resto igual a $0$. Portanto, o polinômio $x-1$ divide o polinômio $x^3-1$. Além disso, o quociente dessa divisão é $q(x) = x^2+x+1$. Também podemos escrever
$$x^3-1 = (x-1) \cdot (x^2+x+1).$$
Exemplo em vídeo:
Viu só como não é difícil dividir polinômios? Basta repetir o mesmo processo visto nestes três exemplos para dividir quaisquer dois polinômios, com o divisor não nulo.
Gostou do conteúdo dessa postagem? Foi útil para você? Tem alguma dúvida? Deixe um comentário.
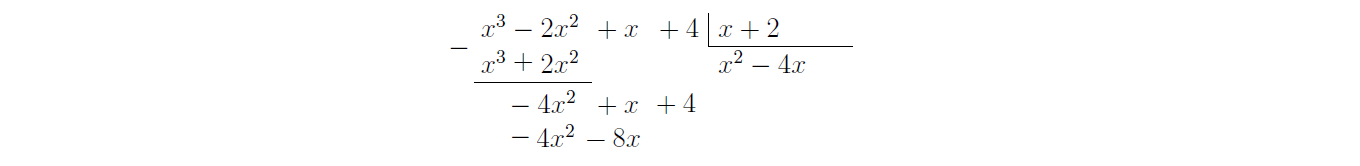
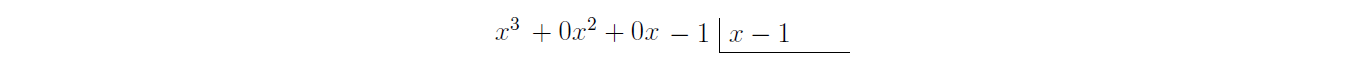
0 Comentários:
Postar um comentário