Nessa série de postagens sobre polinômios, dentre outras coisas, estudamos as operações entre polinômios, o que são raízes de polinômios, algumas formas de obter raízes de polinômios e polinômios irredutíveis. Com esses tópicos bem compreendidos, podemos avançar nosso estudo sobre polinômios e começar a tratar da fatoração de polinômios. Nessa postagem estudaremos o que é a fatoração de um polinômio, quando ela pode ser feita e também veremos, por meio de exemplos, algumas maneiras de fatorar um polinômio. Uma das consequência de se fatorar um polinômio é obter todas as suas raízes, então podemos dizer que obter a fatoraração um polinômio é uma forma de obter todas as suas raízes e isso é muito útil. Faremos isso considerando todos os polinômios sobre $\mathbb{R}$. Vamos lá!
Fatoração de polinômios
Primeiramente vamos entender o que é a fatorar um polinômio e também o que é a fatoração um polinômio.
Fatorar um polinômio $p(x)$ é o processo de escrever esse polinômio como um produto de fatores, ou seja, é o processo de escrever $p(x)$ como um produto de outros polinômios. Cada polinômio desse produto é chamado de fator. A fatoração de um polinômio $p(x)$ é este polinômio escrito como um produto de fatores, isto é, quando se fatora um polinômio $p(x)$, se escreve este polinômio como produto de outros polinômios, este produto de polinômios é chamado fatoração do polinômio $p(x)$.
Podemos considerar dois tipos de fatoração, a fatoração completa e a fatoração incompleta. Uma fatoração de um polinômio $p(x)$ onde todos os fatores são polinômios irredutíveis é chamada fatoração completa de $p(x)$. Caso contrário, a fatoração é chamada fatoração incompleta. Vejamos alguns exemplos.
Exemplos:
1. Podemos escrever o polinômio $p(x) = 3x^3-7x^2-7x+3$ da seguinte maneira
$$3x^3-7x^2-7x+3 = (3x-1)(x+1)(x-3).$$
Essa é uma fatoração do polinômio $p(x)$. Observe que os fatores nessa fatoração são polinômios de grau $1$, ou seja, todos os fatores na fatoração de $p(x)$ são polinômios irredutíveis. Logo essa é uma fatoração completa de $p(x)$.
2. O polinômio $f(x) = 2x^4-2x^2-3x^3+3x$ pode ser escrito na seguinte forma
$$2x^4-2x^2-3x^3+3x = x(2x-3)(x^2-1).$$
Nessa fatoração do polinômio $f(x)$ um dos fatores é o polinômio $x^2-1$ que não é irredutível, pois ele pode ser escrito como $x^2-1 = (x+1)(x-1)$. Logo, a fatoração apresentada acima não é uma fatoração completa do polinômio $f(x)$.
Observação 1: Quando se trata de fatoração de polinômios, os produtos notáveis podem ser muito úteis, vamos lembrá-los
$$(x+a)^2 = x^2+2ax+a^2;$$
$$(x-a)^2 = x^2-2ax+a^2.$$
Além deles, a diferença de quadrados também é muito útil, que é
$$x^2-a^2 = (x+a)(x-a).$$
Note que os dois produtos notáveis e a diferença de quadrados acima são fatorações de polinômios. No exemplo 2 foi usada a diferença de quadrados para escrever $x^2-1=(x+1)(x-1)$ e justificar que a fatoração de $f(x)$ é incompleta.
Por meio desse dois exemplos percebemos que polinômios podem ser fatorados, mas podemos nos perguntar o seguinte: Sempre podemos fatorar um polinômio? O teorema a seguir tem a resposta para essa pergunta.
Teorema: Seja $f(x)$ um polinômio sobre $\mathbb{K}$ ($\mathbb{K} = \mathbb{C}$ ou $\mathbb{K} = \mathbb{R}$). Então, existem polinômios irredutíveis $p_1(x)$, $p_2(x)$, $\dots$, $p_n(x)$ sobre $\mathbb{K}$ tais que
$$f(x) = p_1(x) \cdot p_2(x) \cdot \dots \cdot p_n(x).$$
O que o teorema acima nos diz é, qualquer polinômio sobre $\mathbb{R}$ ou $\mathbb{C}$, possui uma fatoração completa, ou seja, qualquer polinômio sobre esses conjuntos pode ser fatorado. Apesar dessa informação ser muito importante (a existência da fatoração de qualquer polinômio sobre $\mathbb{R}$ ou $\mathbb{C}$), o teorema acima não trás consigo nenhuma informação ou método para fatorar um polinômio. Assim, dado um polinômio $p(x)$, para obtermos a fatoração desse polinômio vamos precisar aplicar tudo o que sabemos sobre raízes de polinômio, sobre métodos para encontrar raízes de polinômios e sobre polinômios irredutíveis. Em geral, não é fácil fatorar um polinômio. Por esse motivo, a seguir veremos alguns exemplos de como podemos fatorar um polinômio com algumas ideias que você pode usar sempre que precisar fatorar um polinômio.
Exemplos:
Nos exemplos a seguir, todos os polinômios serão considerados sobre $\mathbb{R}$.
1. Fatore o polinômio $p(x) = 2x^2+5x-3$.
Solução: Temos que fatorar um polinômio de grau $2$. Como vimos na postagem anterior, esse polinômio pode ser irredutível e, se ele for, não é possivel fatorá-lo. Para verificar se um polinômio de grau $2$ sobre $\mathbb{R}$ é irredutível, precisamos calcular o $\Delta$. Nesse polinômio temos $a=2$, $b=5$ e $c=-3$ e, desse modo
$$\Delta = b^2-4ac = 5^2-4 \cdot 2 \cdot (-3) = 25+24=49.$$
Como $\Delta > 0$, temos que esse polinômio é reditível e, assim, é possível fatorá-lo. Temos algumas formas de fatorar o polinômio $p(x)$. Vamos fazer aqui da maneira "mais difícil" e depois vamos ver forma mais fáceis de fatorar esse polinômio. Vamos primeiramente calcular as raízes desse polinômio. Observe que já calculamos $\Delta$, então, vamos usar a segunda parte da fórmula de Bhaskara para calcular as raízes de $p(x)$. Temos,
$$x = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{-5 \pm \sqrt{49}}{2 \cdot 2} = \frac{-5 \pm 7}{4}.$$
Desse modo, as raízes de $p(x)$ são $\displaystyle\frac{1}{2}$ e $-3$. Pelo que vimos na postagem #6, $p(x)$ é divisível por $x+3$ e por $x - \displaystyle\frac{1}{2}$. Para evitar frações, vamos dividir $p(x)$ por $x-3$ e vamos encontrar o outro fator da fatoração de $p(x)$. Temos,
Fiz o exemplo acima da maneira "mais difícil" por que essa maneira sempre funciona para polinômios redutíveis de grau $2$. Antes de fazermos uma observação com a maneira mais fácil de fatorar um polinômio (redutível) de grau $2$, veremos uma definição.
Definição: Conside um polinômio $f(x)$ sobre $\mathbb{R}$ ou $\mathbb{C}$. O polinômio $f(x)$ é chamado mônico ou unitário se o coeficiente dominante de $p(x)$ for igual a $1$.
Os polinômios $g(x) = x^2-3x-1$ e $h(x) = x^4-2x^3+1$ são exemplos de polinômios mônicos enquanto $r(x) = 2x^3-4x+1$ não é mônico.
Observação 2: Se $f(x)$ é um polinômio mônico de grau $2$, ou seja, se ele possui a forma $p(x) = x^2-a_1x+a_0$ e $\alpha$ e $\beta$ são as suas raízes, então $f(x) = (x-\alpha)(x-\beta)$. Se $\alpha = \beta$, vamos ter o caso do produto notável $f(x) = (x-\alpha)^2$.
Por exemplo, $f(x) = x^2-3x+2$ possui por raízes os números $1$ e $2$ (para verificar isso, podemos usar soma e produto). Desse modo podemos escrever $f(x)$ na forma
$$f(x) = (x-1)(x-2).$$
Mesmo se o polinômio não for mônico, ainda podemos usar o raciocínio acima. No exemplo 1, temos o polinômio $p(x)=2x^2+5x-3$ que não é mônico. Nesse caso, colocamos o coeficiente dominante em evidência, assim vamos ter,
$$p(x) = 2\left(x^2+\frac{5}{2}x-\frac{3}{2}\right).$$
Agora, aplicamos o raciocínio anterior ao polinômio $x^2+\frac{5}{2}x-\frac{3}{2}$ que é mônico. As raízes desse polinômio são $-3$ e $\displaystyle\frac{1}{2}$ (já as calculamos no exemplo 1). Assim, o polinômio $p(x)$ pode ser escrito na forma
$$p(x) = 2\left(x^2+\frac{5}{2}x-\frac{3}{2}\right) = 2(x+3)\left(x-\displaystyle\frac{1}{2}\right).$$
a qual também é uma fatoração de $p(x)$.
Logo, para fatorar um polinômio (redutível) de grau $2$, se você não quiser fazer uma divisão de polinômios como no exemplo 1, basta conhecer suas raízes e usar o raciocínio da observação 2.
De um modo geral, se um polinômio $f(x)$ tem grau $n$, é mônico e possui $n$ raízes $r_1$, $\dots$, $r_n$, então o polinômio $f(x)$ pode ser escrito na forma
$$f(x) = (x-r_1)(x-r_2) \cdots (x-r_n).$$
Vamos continuar com os exemplos.
2. Fatore completamente o polinômio $p(x) = x^3+2x^2+x-4$.
Solução: Vamos começar tentando determinar alguma raiz do polinômio $p(x)$. Pelo Teorema das Raízes Racionais, temos que $\pm 1$, $\pm 2$ e $\pm 4$ são possíveis raízes de $p(x)$. Para verificar se, de fato, algum desses números é uma raíz de $p(x)$, devemos testá-los. Temos
\begin{eqnarray} p(1) &=& 1^3+2 \cdot 1^2 + 1 - 4 \\ &=& 1 + 2+1 - 4 = 0.\end{eqnarray}
Que sorte a nossa! O primeiro número testado já é uma raiz. Bom, poderíamos testar as outras possibilidades para saber se entre elas temos outras raízes, mas não vamos fazer isso. Por que? Como sabemos que $1$ é raiz, então $x-1$ divide $p(x)$. Fazendo essa divisão, vamos encontrar um polinômio $q(x)$ de grau $2$ tal que $p(x) = (x-1)q(x)$ ($q(x)$ terá grau $2$ pois $gr(p(x)) = gr(x-1)+gr(q(x))$, ou seja, $3=1+gr(q(x))$). Assim, para continuar fatorando o polinômio $p(x)$, basta fatorar $q(x)$ que é um polinômio de grau $2$, os quais sabemos bem como fatorar. Dividindo $p(x)$ por $x-1$, temos
Logo, $p(x) = (x-1)(x^2+3x+4)$. Uma fatoração completa é uma fatoração onde todos os fatores são irredutíveis. Assim, para continuar a fatoração de $p(x)$ devemos verificar se $x^2+3x+4$ é irredutível. Se ele for, a fatoração acima já é a que estamos procurardo e, se ele não for, vamos ter que fatorar o polinômio $x^2+3x+4$. Para esse polinômio, temos $a=1$, $b=3$ e $c=4$. Assim,
$$\Delta = b^2-4ac = 3^2-4 \cdot 1 \cdot 4 = 9-16=-7.$$
Como $\Delta < 0$, o polinômio $x^2+3x+4$ é irredutível e a fatoração $p(x) = (x-1)(x^2+3x+4)$ de $p(x)$ é uma fatoração completa.
Antes do próximo exemplo, temos outra observação importante.
Observação 3: Considere $f(x)$ um polinômio qualquer. Se a somas dos seus coeficientes for igual a $0$, então o número $1$ é raiz de $p(x)$.
Essa observação poderia ser usada para calcular a raiz de $p(x)$ do exemplo 2. Sempre que for calcular as raízes de um polinômio, sempre verifique se a soma de seus seus coeficientes é igual a $0$, pois se for, já terá o número $1$ como raiz desse polinômio.
Vamos para o próximo exemplo.
3. Determine a fatoração completa do polinômio $p(x) = x^3-7x-6$.
Solução: Os coeficientes do polinômio $p(x)$ são $1$, $-7$ e $-6$ e, como $1-7-6 = -12 \neq 0$, segue que $1$ não é raiz de $p(x)$. Vamos aplicar nesse polinômio o Teorema das Raízes Racionais. Por esse teorema, as possibilidades de raízes de $p(x)$ são $\pm 1$, $\pm 2$, $\pm 3$ e $\pm 6$. Como $1$ não é raiz de $p(x)$, vamos começar a testar as possibilidades de raízes pelo $-1$. Temos,
$$p(-1) = (-1)^3-7 \cdot (-1)-6 = -1+7-6=0.$$
Já encontramos uma raiz de $p(x)$, o $-1$. Assim, $p(x)$ é divisível por $x+1$. Fazendo a divisão, temos
Logo, $p(x) = (x+1)(x^2-x-6)$. Para continuar a fatoração de $p(x)$, vamos fatorar $x^2-x-6$. Usando soma e produto, temos que este polinômio possui as raízes $-2$ e $3$ (ele é redutível). Desse modo, como $x^2-x-6$ é mônico, segue que $x^2-x-6=(x+2)(x-3)$. Portanto, a fatoração completa de $p(x)$ é $p(x)= (x+1)(x+2)(x-3)$.
4. Encontre a fatoração completa do polinômio $p(x) = x^4+3x^3+3x^2+3x+2$.
Solução: Claramante, $1$ não raiz do polinômio $p(x)$. Como esse polinômio possui grau $4$, vamos novamente usar o Teorema das Raízes Racionais. Desse modo, as possibilidade de raízes são $\pm 1$ e $\pm 2$. Como já sabemos que $1$ não é raiz, vamos prosseguir testando o $-1$. Temos,
\begin{eqnarray} p(-1) &=& (-1)^4+3 \cdot (-1)^3 + 3 \cdot (-1)^2 + 3 \cdot (-1) + 1 \\ &=& 1 -3+3-3+2 = 0. \end{eqnarray}
Logo, $-1$ é raiz de $p(x)$. Vamos agora dividir $p(x)$ por $x+1$. Temos
Logo, $p(x) = (x+1)(x^3+2x^2+x+2)$. Agora temos que continuar fatorando o polinômio $q(x) = x^3+2x^2+x+2$. Vamos novamente aplicar o Teorema das raízes racionais nesse polinômio. Desse modo, suas possíveis raízes são $\pm 1$ e $\pm 2$. E fácil ver que $1$ não é raiz. Assim, vamos testar as outras posibilidades. Temos
\begin{eqnarray} q(-1) &=& (-1)^3+2 \cdot (-1)^2 + (-1)+2 \\ &=& -1 + 2- 1 +2 = 2 \end{eqnarray}
\begin{eqnarray} q(2) &=& 2^3+2 \cdot 2^2 + 2 +2 \\ &=& 8 + 8 + 2 +2 = 20 \end{eqnarray}
\begin{eqnarray} q(-2) &=& (-2)^3+2 \cdot (-2)^2 + (-2)+2 \\ &=& -8 + 8- 2 +2 = 0 \end{eqnarray}
Logo, $-2$ é raiz de $q(x)$ e $q(x)$ é divisível por $x+2$. Fazendo a divisão, temos
Assim, $q(x) = (x+2)(x^2+1)$. Escrevendo $q(x)$ dessa forma, temos que $p(x) = (x+1)(x+2)(x^2+1)$. Observe que $x^2+1$ é irredutível, pois esse polinômio possui $\Delta = -4 < 0$. Logo, $p(x) = (x+1)(x+2)(x^2+1)$ é uma fatoração completa.
5. Determine a fatoração completa do polinômio $p(x) = x^4+2x^3+2x^2$.
Solução: Vamos fazer esse exemplo de uma forma diferente. Antes de tentar usar o Teorema das Raízes Racionais, podemos tentar reescrever o polinômio já determinando a sua forma fatorada. Observe que podemos colocar o $x^2$ em evidência no polinômio $p(x)$ e, assim, temos
$$p(x) = x^2(x^2 + 2x+ 1).$$
Agora, observe que $x^2+2x+1 = (x+1)^2$, logo
$$p(x) = x^2(x+1)^2.$$
Essa é a fatoração completa de $p(x)$, pois é um produto de polinômio de grau $1$ ($p(x) = x x (x+1)(x+1)$).
Então, antes de pensar um uma conta mais complicada ou uma forma mais complexa de fatorar um polinômio, tente reescrevê-lo em forma de produto colocando algum termo em evidência. Isso pode simplificar bastate o processo de fatorar um polinômio.
Vamos usar esse mesmo raciocínio no próximo exemplo (um pouco mais complicado).
6. Fatore completamente o polinômio $p(x) = x^5-x^4-5x^3+5x^2+4x-4$.
Solução: Podemos reescrever esse polinômio na seguinte forma
\begin{eqnarray} x^5-x^4-5x^3+5x^2+4x-4 &=& x^5-x^4-x^3+x^2 - 4x^3+4x^2+4x-4 \\ &=& x^2(x^3-x^2-x+1) -4(x^3-x^2-x+1) \\ &=& (x^2-4)(x^3-x^2-x+1) \\ &=& (x^2-4)(x^3-2x^2+x+x^2-2x+1) \\ &=& (x^2-4)(x(x^2-2x+1) + (x^2-2x+1)) \\ &=& (x^2-4)(x+1)(x^2-2x+1) \\ &=& (x^2-4)(x+1)(x-1)^2 \\ &=& (x-2)(x+2)(x+1)(x-1)^2 \end{eqnarray}
Logo, a fatoração de completa de $p(x)$ é
$$p(x) = (x-2)(x+2)(x+1)(x-1)^2.$$
Raramente a ideia utilizada no exemplo 6 é fácil de ser aplicada, mas é uma tentativa a ser considerada.
Esses 6 exemplos contém ideias para fatorar polinômios que são muito úteis. Se você estudar esses exemplos e aplicar as mesmas ideias a outros polinômio, a chance de você conseguir fatorá-lo é muito grande.
Por último, um exemplo em vídeo:
Gostou do conteúdo dessa postagem? Foi útil para você? Tem alguma dúvida? Deixe um comentário.





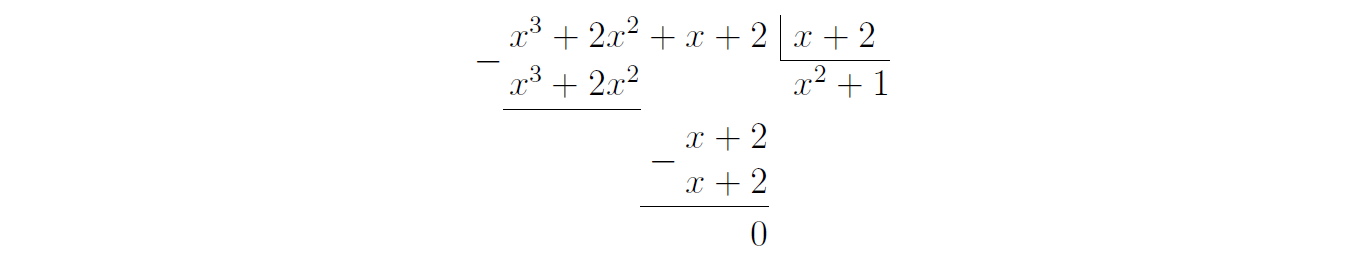
0 Comentários:
Postar um comentário